Frequency Discrimination Method for Generating SSB Modulated Wave

The frequency discrimination method for generating SSB (Single Sideband) modulated wave is a method that uses a phase shift network and a bandpass filter to produce a single sideband signal without the carrier frequency. This method is also known as the filter method or the phase shift method.

The basic idea behind this method is to shift the phase of the modulating signal by 90 degrees using a phase shift network, and then to filter out one of the sidebands using a bandpass filter. The resulting signal is a single sideband signal with the carrier frequency suppressed.

The frequency discrimination method can be implemented using the following steps:
1.The modulating signal is first applied to a phase shift network that introduces a phase shift of 90 degrees.

2. This phase shift network can be implemented using a simple circuit such as a RC network or a LC network.

3. The output of the phase shift network is then mixed with the carrier signal to produce a double sideband suppressed carrier (DSB-SC) signal.The DSB-SC signal is then passed through a bandpass filter that has a passband centered around the desired frequency. The bandpass filter is designed to attenuate one of the sidebands and pass the other sideband, along with the carrier frequency.

 4. The output of the bandpass filter is a single sideband signal with the carrier frequency suppressed. The single sideband signal can be amplified and transmitted over the communication channel.

The frequency discrimination method for generating SSB modulated wave is a popular method in radio communication applications due to its simplicity and efficiency. However, it does have some limitations, such as a lower power efficiency compared to other SSB generation methods, and the need for careful tuning of the bandpass filter to achieve good selectivity.
 

Consider the generation of SSB modulated signal containing the upper side band only. From a practical point of view, the most severe requirement of SSB generation arises from the unwanted sideband, the nearest component of which is separated from the desired side band by twice the lowest frequency component of the message signal. It implies that, for the generation of an SSB wave to be possible,
the message spectrum must have an energy gap centered at the origin as shown infigure 7. This requirement is naturally satisfied by voice signals, whose energy gap is about 600Hz wide.

The frequency discrimination or filter method of SSB generation consists of a product modulator, which produces DSBSC signal and a band-pass filter to extract the desired side band and reject the other and is shown in the figure 8.
 

frequency discrimination of SSB generation wave

Application of this method requires that the message signal satisfies two conditions:
1. The message signal m(t) has no low-frequency content. Example: speech, audio,
music.
2. The highest frequency component W of the message signal m(t) is much less
than the carrier frequency fc.
Then, under these conditions, the desired side band will appear in a non overlapping interval in the spectrum in such a way that it may be selected by an appropriate filter.
In designing the band pass filter, the following requirements should be satisfied:
1. The pass band of the filter occupies the same frequency range as the spectrum of the desired SSB modulated wave.
2. The width of the guard band of the filter, separating the pass band from the stop band, where the unwanted sideband of the filter input lies, is twice the lowest frequency component of the message signal.
When it is necessary to generate an SSB modulated wave occupying a frequency band that is much higher than that of the message signal, it becomes very difficult to design an appropriate filter that will pass the desired side band and reject the other. In such a situation it is necessary to resort to a multiple-modulation process so as to ease the filtering requirement. This approach is illustrated in the following figure 9 involving two stages of modulation.

Two stage Frequency Discriminator

The SSB modulated wave at the first filter output is used as the modulating wave for the second product modulator, which produces a DSBSC modulated wave with a spectrum that is symmetrically spaced about the second carrier frequency f2. The frequency separation between the side bands of this DSBSC modulated wave is effectively twice the first carrier frequency f1, thereby permitting the second filter to
remove the unwanted side band.

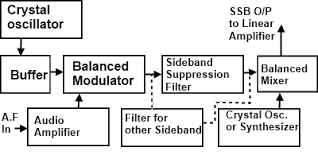filter method of ssb

Advantages and disadvantages filter method

The filter method, also known as the frequency discrimination method, is a simple and widely used technique for generating SSB (Single Sideband) modulated wave. The filter method has several advantages and disadvantages, which are outlined below:

Advantages:

    Simplicity: The filter method requires only a phase shift network and a bandpass filter, which makes it simple and easy to implement.

    Bandwidth efficiency: The filter method produces a narrowband signal that has a bandwidth equal to the message bandwidth, which results in higher spectral efficiency compared to other modulation techniques such as AM (Amplitude Modulation).

    High quality of the transmitted signal: The filter method results in a high-quality transmitted signal with reduced noise and interference, as it eliminates the carrier and one of the sidebands that can cause interference.

Disadvantages:

    Lower power efficiency: The filter method is less power-efficient than other SSB generation methods such as the Weaver method, as the filter method results in power loss due to the attenuation of the unwanted sideband by the bandpass filter.

    Selectivity issues: The filter method requires careful tuning of the bandpass filter to achieve good selectivity and minimize interference from neighboring channels.

    Limited frequency range: The filter method is suitable only for narrowband communication applications and cannot be used for high-frequency signals due to the limitations of the bandpass filter.

Overall, the filter method is a simple and efficient technique for generating SSB modulated wave, but it may have limitations in terms of power efficiency and frequency range, and requires careful tuning of the bandpass filter.

Properties:

1. A signal 𝑥(𝑡) and its Hilbert transform 𝑥 ̂(𝑡) have the same amplitude spectrum. The
magnitude of −𝑗𝑠𝑔𝑛(𝑓) is equal to 1 for all frequencies f. Therefore x(t) and 𝑥 ̂(𝑡) have the same amplitude spectrum. That is |𝑋 ̂(𝑓)| = |𝑋(𝑓)| 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑓
2. If 𝑥 ̂(𝑡) is the Hilbert transform of x(t), then the Hilbert transform of 𝑥 ̂(𝑡)𝑖𝑠 − 𝑥(𝑡). To
obtain its Hilbert transform of x(t), x(t) is passed through LTI system with a transfer
function equal to −𝑗𝑠𝑔𝑛(𝑓). A double Hilbert transformation is equivalent to passing 𝑥(𝑡) through a cascade of two such devices. The overall transfer function of such a cascade is equal to [−𝑗𝑠𝑔𝑛(𝑓)]2 = −1 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑓 The resulting output is −𝑥(𝑡). That is the Hilbert transform of 𝑥 ̂(𝑡)is equal to −𝑥(𝑡).